Multi-Scale Graph Learning for Anti-Sparse Downscaling

Water temperature can vary substantially even across short distances within the same sub-watershed. Accurate prediction of stream water temperature at fine spatial resolutions (i.e., fine scales, $\leq$ 1 km) enables precise interventions to maintain water quality and protect aquatic habitats. Although spatiotemporal models have made substantial progress in spatially coarse time series modeling, challenges persist in predicting at fine spatial scales due to the lack of data at that scale.To address the problem of insufficient fine-scale data, we propose a Multi-Scale Graph Learning (MSGL) method. This method employs a multi-task learning framework where coarse-scale graph learning, bolstered by larger datasets, simultaneously enhances fine-scale graph learning. Although existing multi-scale or multi-resolution methods integrate data from different spatial scales, they often overlook the spatial correspondences across graph structures at various scales. To address this, our MSGL introduces an additional learning task, cross-scale interpolation learning, which leverages the hydrological connectedness of stream locations across coarse- and fine-scale graphs to establish cross-scale connections, thereby enhancing overall model performance. Furthermore, we have broken free from the mindset that multi-scale learning is limited to synchronous training by proposing an Asynchronous Multi-Scale Graph Learning method (ASYNC-MSGL). Extensive experiments demonstrate the state-of-the-art performance of our method for anti-sparse downscaling of daily stream temperatures in the Delaware River Basin, USA, highlighting its potential utility for water resources monitoring and management.

Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

Predicting Water Temperature Dynamics of Unmonitored Lakes with Meta Transfer Learning

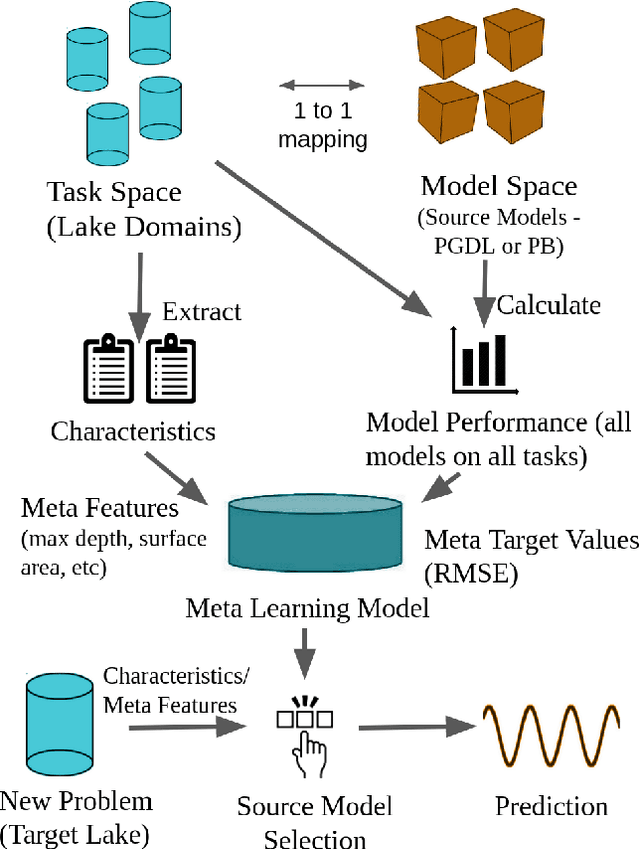
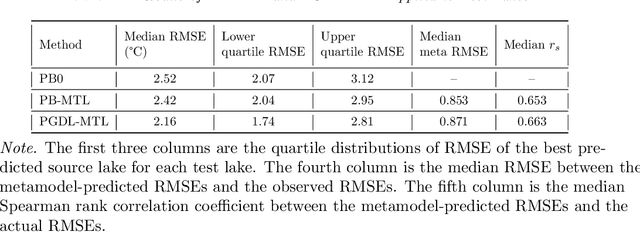
Most environmental data come from a minority of well-observed sites. An ongoing challenge in the environmental sciences is transferring knowledge from monitored sites to unobserved sites. Here, we demonstrate a novel transfer learning framework that accurately predicts temperature in unobserved lakes (targets) by borrowing models from highly observed lakes (sources). This method, Meta Transfer Learning (MTL), builds a meta-learning model to predict transfer performance from candidate source models to targets using lake attributes and candidates' past performance. We constructed source models at 145 well-observed lakes using calibrated process-based modeling (PB) and a recently developed approach called process-guided deep learning (PGDL). We applied MTL to either PB or PGDL source models (PB-MTL or PGDL-MTL, respectively) to predict temperatures in 305 target lakes treated as unobserved in the Upper Midwestern United States. We show significantly improved performance relative to the uncalibrated process-based General Lake Model, where the median RMSE for the target lakes is $2.52^{\circ}C$. PB-MTL yielded a median RMSE of $2.43^{\circ}C$; PGDL-MTL yielded $2.16^{\circ}C$; and a PGDL-MTL ensemble of nine sources per target yielded $1.88^{\circ}C$. For sparsely observed target lakes, PGDL-MTL often outperformed PGDL models trained on the target lakes themselves. Differences in maximum depth between the source and target were consistently the most important predictors. Our approach readily scales to thousands of lakes in the Midwestern United States, demonstrating that MTL with meaningful predictor variables and high-quality source models is a promising approach for many kinds of unmonitored systems and environmental variables.

Physics-Guided Architecture (PGA) of Neural Networks for Quantifying Uncertainty in Lake Temperature Modeling

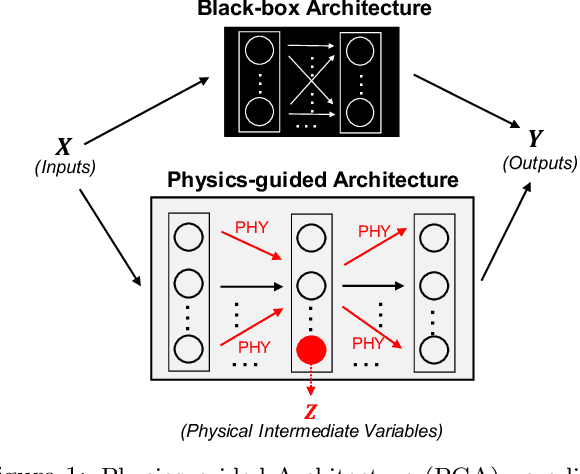
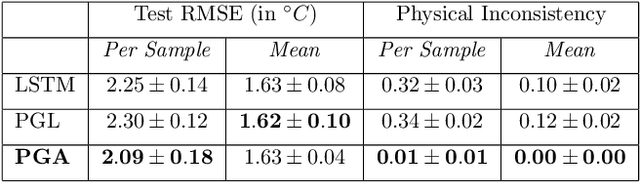
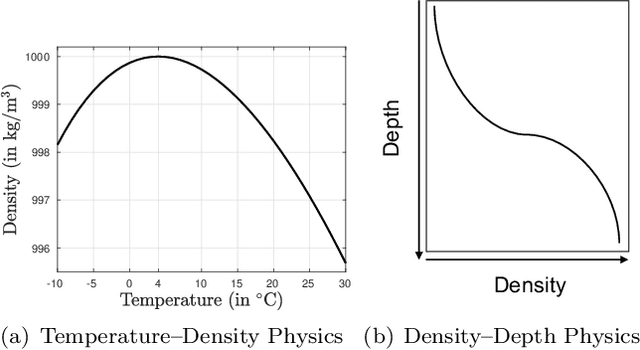
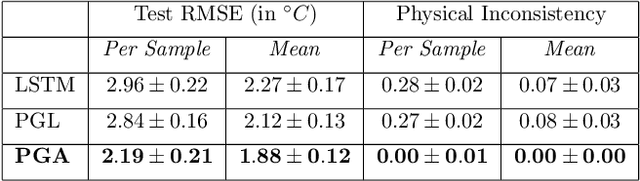
To simultaneously address the rising need of expressing uncertainties in deep learning models along with producing model outputs which are consistent with the known scientific knowledge, we propose a novel physics-guided architecture (PGA) of neural networks in the context of lake temperature modeling where the physical constraints are hard coded in the neural network architecture. This allows us to integrate such models with state of the art uncertainty estimation approaches such as Monte Carlo (MC) Dropout without sacrificing the physical consistency of our results. We demonstrate the effectiveness of our approach in ensuring better generalizability as well as physical consistency in MC estimates over data collected from Lake Mendota in Wisconsin and Falling Creek Reservoir in Virginia, even with limited training data. We further show that our MC estimates correctly match the distribution of ground-truth observations, thus making the PGA paradigm amenable to physically grounded uncertainty quantification.